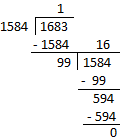Algebra and General Mathematics: Multiple

MULTIPLE

A multiple is a number made by multiplying together two other numbers.

COMMON MULTIPLE

A whole number which is a multiple of a group of numbers.

Example:

Find the multiples of 3 and 6 that are greater than 12 but less than 24.

Solution:

Multiples of 3 greater than 12 but less than 30:

= { 15, 18, 21, 24, 27 }

Multiples of 6 greater than 12 but less than 30:

= { 18, 24 }

Therefore, the common multiples of 3 and 6 are:

M3 ⋂ M6 = { 18, 24 }

LEAST COMMON MULTIPLE (LCM)

The lowest common multiple (LCM) of two whole numbers is the smallest whole number which is a multiple of both.

Example:

Find the LCM of 240, 600 and 720.

Solution:

-get all the prime factors of the numbers in canonical form

F(240)  = 3 x 5 x 24

F(600)  = 3 x 52 x 23

F(720)  = 32 x 5 x 24

Therefore, the LCM is:

LCM = 24 x 32 x 52 = 3600

Relationship between HCF and LCM of two numbers:

The product of two numbers is equal to the product of their Highest Common Factor and Least Common Multiple.

First number x Second number = (HCM)(LCM)

Proof:

For numbers 15 and 18, proof the relationship between HCF and LCM.

HCF of 15 and 18:

F(15) = { 3, 5 }

F(18) = { 2, 32 }

Thus, HCF is equal to 3

LCM of 15 and 18

F(15) = { 3, 5 }

F(18) = { 2, 32 }

Thus, LCM is equal to:

LCM = 2 x 32 x 5

Thus, LCM is equal to 90

Therefore,

15 x 18 = 3 x 90

= 270 (proven)

Solved examples on the relationship between HCF and LCM.:

1. Find the L.C.M. of 1683 and 1584.

First we find highest common factor of 1683 and 1584.                     

Thus, highest common factor of 1683 and 1584 = 99

Lowest common multiple of 1683 and 1584 = First number × Second number/ H.C.F.

= 1584 × 1683/99

Therefore, LCM is 26,928

2. Highest common factor and lowest common multiple of two numbers are 15 and 1980 respectively. One number is 150, find the other.

We know, H.C.F. × L.C.M. = First number × Second number then we get,

15 × 1980 = 150 × Second number

(15 × 1980) / 150 = Second number

Therefore, the second number = 198

3. The highest common factor and the lowest common multiple of two numbers are 925 and 50 respectively. If one of the two numbers is 250, find the other number.

We know, H.C.F. × L.C.M. = First number × Second number then we get,

925 × 50 = 250 × Second number

(925 × 50) / 250 = Second number

Therefore, the second number = 185